Website - Youtube - About - Talks - Books - Packages - RSS

Intrumental variable regression and machine learning

R
econometrics
Published

November 9, 2019

Intro

Just like the question “what’s the difference between machine learning and statistics” has shed a lot of ink (since at least Breiman (2001)), the same question but where statistics is replaced by econometrics has led to a lot of discussion, as well. I like this presentation by Hal Varian from almost 6 years ago. There’s a slide called “What econometrics can learn from machine learning”, which summarises in a few bullet points Varian (2014) and the rest of the presentation discusses what machine learning can learn from econometrics. Varian argues that the difference between machine learning and econometrics is that machine learning focuses on prediction, while econometrics on inference and causality (and to a lesser extent prediction as well). Varian cites some methods that have been in the econometricians’ toolbox for decades (at least for some of them), such as regression discontinuity, difference in differences and instrumental variables regression. Another interesting paper is Mullainathan and Spiess, especially the section called What Do We (Not) Learn from Machine Learning Output?. The authors discuss the tempting idea of using LASSO to perform variable (feature) selection. Econometricians might be tempted to use LASSO to perform variable selection, and draw conclusions such as The variable (feature) “Number of rooms” has not been selected by LASSO, thus it plays no role in the prediction of house prices. However, when variables (features) are highly correlated, LASSO selects variables essentially randomly, without any meaningful impact on model performance (for prediction). I found this paragraph quite interesting (emphasis mine):

This problem is ubiquitous in machine learning. The very appeal of these algorithms is that they can fit many different functions. But this creates an Achilles’ heel: more functions mean a greater chance that two functions with very different coefficients can produce similar prediction quality. As a result, how an algorithm chooses between two very different functions can effectively come down to the flip of a coin. In econometric terms, while the lack of standard errors illustrates the limitations to making inference after model selection, the challenge here is (uniform) model selection consistency itself.

Assuming that we successfully dealt with model selection, we still have to content with significance of coefficients. There is recent research into this topic, such as Horel and Giesecke, but I wonder to what extent explainability could help with this. I have been looking around for papers that discuss explainability in the context of the social sciences but have not found any. If any of the readers of this blog are aware of such papers, please let me know.

Just to wrap up Mullainathan and Spiess; the authors then suggest to use machine learning mainly for prediction tasks, such as using images taken using satellites to predict future harvest size (the authors cite Lobell (2013)), or for tasks that have an implicit prediction component. For instance in the case of instrumental variables regression, two stages least squares is often used, and the first stage is a prediction task. Propensity score matching is another prediction task, where machine learning could be used. Other examples are presented as well. In this blog post, I’ll explore two stages least squares and see what happens when a random forest is used for the first step.

Instrumental variables regression using two-stage least squares

Let’s work out a textbook (literally) example of instrumental variable regression. The below example is taken from Wooldrige’s Econometric analysis of cross section and panel data, and is an exercise made using data from Mroz (1987) The sensitivity of an empirical model of married women’s hours of work to economic and statistical assumptions.

Let’s first load the needed packages and the data "mroz" included in the {wooldridge} package: 

library(tidyverse)
library(randomForest)
library(wooldridge)
library(AER)
library(Metrics)

data("mroz")

Let’s only select the women that are in the labour force (inlf == 1), and let’s run a simple linear regression. The dependent variable, or target, is lwage, the logarithm of the wage, and the explanatory variables, or features are exper, expersq and educ. For a full description of the data, click below:

Description of data 


mroz {wooldridge}   R Documentation
mroz

Description

Wooldridge Source: T.A. Mroz (1987), “The Sensitivity of an Empirical Model of Married Women’s Hours of Work to Economic and Statistical Assumptions,” Econometrica 55, 765-799. Professor Ernst R. Berndt, of MIT, kindly provided the data, which he obtained from Professor Mroz. Data loads lazily.

Usage

data('mroz')
Format

A data.frame with 753 observations on 22 variables:

inlf: =1 if in lab frce, 1975

hours: hours worked, 1975

kidslt6: # kids < 6 years

kidsge6: # kids 6-18

age: woman's age in yrs

educ: years of schooling

wage: est. wage from earn, hrs

repwage: rep. wage at interview in 1976

hushrs: hours worked by husband, 1975

husage: husband's age

huseduc: husband's years of schooling

huswage: husband's hourly wage, 1975

faminc: family income, 1975

mtr: fed. marg. tax rte facing woman

motheduc: mother's years of schooling

fatheduc: father's years of schooling

unem: unem. rate in county of resid.

city: =1 if live in SMSA

exper: actual labor mkt exper

nwifeinc: (faminc - wage*hours)/1000

lwage: log(wage)

expersq: exper^2

Used in Text

pages 249-251, 260, 294, 519-520, 530, 535, 535-536, 565-566, 578-579, 593- 595, 601-603, 619-620, 625

Source

https://www.cengage.com/cgi-wadsworth/course_products_wp.pl?fid=M20b&product_isbn_issn=9781111531041


working_w <- mroz %>% 
    filter(inlf == 1)

wage_lm <- lm(lwage ~ exper + expersq + educ, 
              data = working_w)

summary(wage_lm)
## 
## Call:
## lm(formula = lwage ~ exper + expersq + educ, data = working_w)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.08404 -0.30627  0.04952  0.37498  2.37115 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.5220406  0.1986321  -2.628  0.00890 ** 
## exper        0.0415665  0.0131752   3.155  0.00172 ** 
## expersq     -0.0008112  0.0003932  -2.063  0.03974 *  
## educ         0.1074896  0.0141465   7.598 1.94e-13 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6664 on 424 degrees of freedom
## Multiple R-squared:  0.1568, Adjusted R-squared:  0.1509 
## F-statistic: 26.29 on 3 and 424 DF,  p-value: 1.302e-15

Now, we see that education is statistically significant and the effect is quite high. The return to education is about 11%. Now, let’s add some more explanatory variables: 

wage_lm2 <- lm(lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage + city + educ, 
              data = working_w)

summary(wage_lm2)
## 
## Call:
## lm(formula = lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + 
##     huswage + city + educ, data = working_w)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.07431 -0.30500  0.05477  0.37871  2.31157 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.3853695  0.3163043  -1.218  0.22378    
## exper        0.0398817  0.0133651   2.984  0.00301 ** 
## expersq     -0.0007400  0.0003985  -1.857  0.06402 .  
## kidslt6     -0.0564071  0.0890759  -0.633  0.52692    
## kidsge6     -0.0143165  0.0276579  -0.518  0.60499    
## husage      -0.0028828  0.0049338  -0.584  0.55934    
## huswage      0.0177470  0.0102733   1.727  0.08482 .  
## city         0.0119960  0.0725595   0.165  0.86877    
## educ         0.0986810  0.0151589   6.510 2.16e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6669 on 419 degrees of freedom
## Multiple R-squared:  0.1654, Adjusted R-squared:  0.1495 
## F-statistic: 10.38 on 8 and 419 DF,  p-value: 2.691e-13

The return to education lowers a bit, but is still significant. Now, the issue is that education is not exogenous (randomly assigned), and is thus correlated with the error term of the regression, due to an omitted variable for instance contained in the error term, that is correlated with education (for example work ethic).

To deal with this, econometricians use instrumental variables (IV) regression. I won’t go into detail here; just know that this method can deal with these types of issues. The Wikipedia page gives a good intro on what this is all about. This short paper is also quite interesting in introducing instrumental variables.

In practice, IV is done in two steps. First, regress the endogenous variable, in our case education, on all the explanatory variables from before, plus so called instruments. Instruments are variables that are correlated with the endogenous variable, here education, but uncorrelated to the error term. They only affect the target variable through their correlation with the endogenous variable. We will be using the education level of the parents of the women, as well as the education levels of their husbands as intruments. The assumption is that the parents’, as well as the husband’s education are exogenous in the log wage of the woman. This assumption can of course be challenged, but let’s say that it holds.

To conclude stage 1, we obtain the predictions of education: 

first_stage <- lm(educ ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage 
                  + city + motheduc +  fatheduc + huseduc, data = working_w)

working_w$predictions_first_stage <- predict(first_stage)

We are now ready for the second stage. In the regression from before: 

wage_lm2 <- lm(lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage + city + educ, 
              data = working_w)

we now replace educ with the predictions of stage 1: 

second_stage <- lm(lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage 
                   + city + predictions_first_stage,
                  data = working_w)

summary(second_stage)
## 
## Call:
## lm(formula = lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + 
##     huswage + city + predictions_first_stage, data = working_w)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.13493 -0.30004  0.03046  0.37142  2.27199 
## 
## Coefficients:
##                           Estimate Std. Error t value Pr(>|t|)   
## (Intercept)              0.1763588  0.4206911   0.419   0.6753   
## exper                    0.0419047  0.0139885   2.996   0.0029 **
## expersq                 -0.0007881  0.0004167  -1.891   0.0593 . 
## kidslt6                 -0.0255934  0.0941128  -0.272   0.7858   
## kidsge6                 -0.0234422  0.0291914  -0.803   0.4224   
## husage                  -0.0042628  0.0051919  -0.821   0.4121   
## huswage                  0.0263802  0.0114511   2.304   0.0217 * 
## city                     0.0215685  0.0759034   0.284   0.7764   
## predictions_first_stage  0.0531993  0.0263735   2.017   0.0443 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6965 on 419 degrees of freedom
## Multiple R-squared:  0.08988,    Adjusted R-squared:  0.0725 
## F-statistic: 5.172 on 8 and 419 DF,  p-value: 3.581e-06

We see that education, now instrumented by the parents’ and the husband’s education is still significant, but the effect is much lower. The return to education is now about 5%. However, should our assumption hold, this effect is now causal. However there are some caveats. The IV estimate is a local average treatment effect, meaning that we only get the effect on those individuals that were affected by the treatment. In this case, it would mean that the effect we recovered is only for women who were not planning on, say, studying, but only did so under the influence of their parents (or vice-versa).

IV regression can also be achieved using the ivreg() function from the {AER} package: 

inst_reg <- ivreg(lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage + city + educ 
                  | .-educ + motheduc + fatheduc + huseduc,
                  data = working_w)

summary(inst_reg)
## 
## Call:
## ivreg(formula = lwage ~ exper + expersq + kidslt6 + kidsge6 + 
##     husage + huswage + city + educ | . - educ + motheduc + fatheduc + 
##     huseduc, data = working_w)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.10175 -0.30407  0.03379  0.35255  2.25107 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)   
## (Intercept)  0.1763588  0.4071522   0.433   0.6651   
## exper        0.0419047  0.0135384   3.095   0.0021 **
## expersq     -0.0007881  0.0004033  -1.954   0.0514 . 
## kidslt6     -0.0255934  0.0910840  -0.281   0.7789   
## kidsge6     -0.0234422  0.0282519  -0.830   0.4071   
## husage      -0.0042628  0.0050249  -0.848   0.3967   
## huswage      0.0263802  0.0110826   2.380   0.0177 * 
## city         0.0215685  0.0734606   0.294   0.7692   
## educ         0.0531993  0.0255247   2.084   0.0377 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6741 on 419 degrees of freedom
## Multiple R-Squared: 0.1475,  Adjusted R-squared: 0.1312 
## Wald test: 5.522 on 8 and 419 DF,  p-value: 1.191e-06

Ok, great, now let’s see how a machine learning practitioner who took an econometrics MOOC might tackle the issue. The first step will be to split the data into training and testing sets: 

set.seed(42)
sample <- sample.int(n = nrow(working_w), size = floor(.90*nrow(working_w)), replace = F)
train <- working_w[sample, ]
test  <- working_w[-sample, ]

Let’s now run the same analysis as above, but let’s compute the RMSE of the first stage regression on the testing data as well: 

first_stage <- lm(educ ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage 
                  + city + motheduc +  fatheduc + huseduc, data = train)

test$predictions_first_stage <- predict(first_stage, newdata = test)

lm_rmse <- rmse(predicted = test$predictions_first_stage, actual = test$educ)

train$predictions_first_stage <- predict(first_stage)

The first stage is done, let’s go with the second stage: 

second_stage <- lm(lwage ~ exper + expersq + kidslt6 + kidsge6 + 
                       husage + huswage + city + predictions_first_stage,
                  data = train)

summary(second_stage)
## 
## Call:
## lm(formula = lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + 
##     huswage + city + predictions_first_stage, data = train)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.09828 -0.28606  0.05248  0.37258  2.29947 
## 
## Coefficients:
##                           Estimate Std. Error t value Pr(>|t|)   
## (Intercept)             -0.0037711  0.4489252  -0.008  0.99330   
## exper                    0.0449370  0.0145632   3.086  0.00218 **
## expersq                 -0.0008394  0.0004344  -1.933  0.05404 . 
## kidslt6                 -0.0630522  0.0963953  -0.654  0.51345   
## kidsge6                 -0.0197164  0.0306834  -0.643  0.52089   
## husage                  -0.0034744  0.0054358  -0.639  0.52310   
## huswage                  0.0219622  0.0118602   1.852  0.06484 . 
## city                     0.0679668  0.0804317   0.845  0.39863   
## predictions_first_stage  0.0618777  0.0283253   2.185  0.02954 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6952 on 376 degrees of freedom
## Multiple R-squared:  0.1035, Adjusted R-squared:  0.08438 
## F-statistic: 5.424 on 8 and 376 DF,  p-value: 1.764e-06

The coefficients here are a bit different due to the splitting, but that’s not an issue. Ok, great, but our machine learning engineer is in love with random forests, so he wants to use a random forest for the prediction task of the first stage: 

library(randomForest)

first_stage_rf <- randomForest(educ ~ exper + expersq + kidslt6 + kidsge6 + husage + huswage 
                  + city + motheduc +  fatheduc + huseduc, 
                               data = train)

test$predictions_first_stage_rf <- predict(first_stage_rf, newdata = test)

rf_rmse <- rmse(predicted = test$predictions_first_stage_rf, actual = test$educ)

train$predictions_first_stage_rf <- predict(first_stage_rf)

Let’s compare the RMSE’s of the two first stages. The RMSE of the first stage using linear regression was 2.0558723 and for the random forest 2.0000417. Our machine learning engineer is happy, because the random forest has better performance. Let’s now use the predictions for the second stage: 

second_stage_rf_lm <- lm(lwage ~ exper + expersq + kidslt6 + kidsge6 + 
                             husage + huswage + city + predictions_first_stage_rf,
                  data = train)

summary(second_stage_rf_lm)
## 
## Call:
## lm(formula = lwage ~ exper + expersq + kidslt6 + kidsge6 + husage + 
##     huswage + city + predictions_first_stage_rf, data = train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.0655 -0.3198  0.0376  0.3710  2.3277 
## 
## Coefficients:
##                              Estimate Std. Error t value Pr(>|t|)   
## (Intercept)                -0.0416945  0.4824998  -0.086  0.93118   
## exper                       0.0460311  0.0145543   3.163  0.00169 **
## expersq                    -0.0008594  0.0004344  -1.978  0.04863 * 
## kidslt6                    -0.0420827  0.0952030  -0.442  0.65872   
## kidsge6                    -0.0211208  0.0306490  -0.689  0.49117   
## husage                     -0.0033102  0.0054660  -0.606  0.54514   
## huswage                     0.0229111  0.0118142   1.939  0.05322 . 
## city                        0.0688384  0.0805209   0.855  0.39314   
## predictions_first_stage_rf  0.0629275  0.0306877   2.051  0.04100 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6957 on 376 degrees of freedom
## Multiple R-squared:  0.1021, Adjusted R-squared:  0.08302 
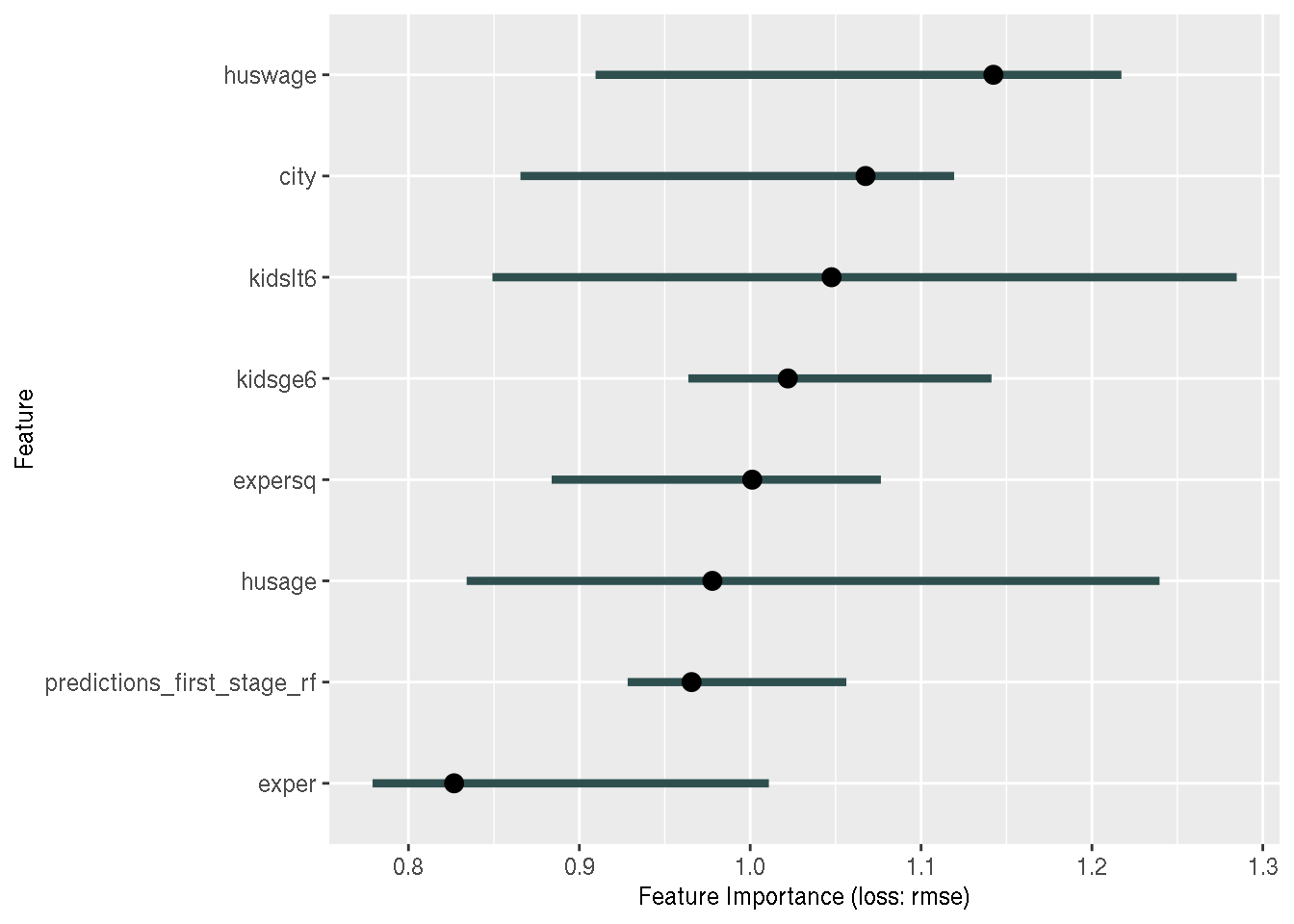
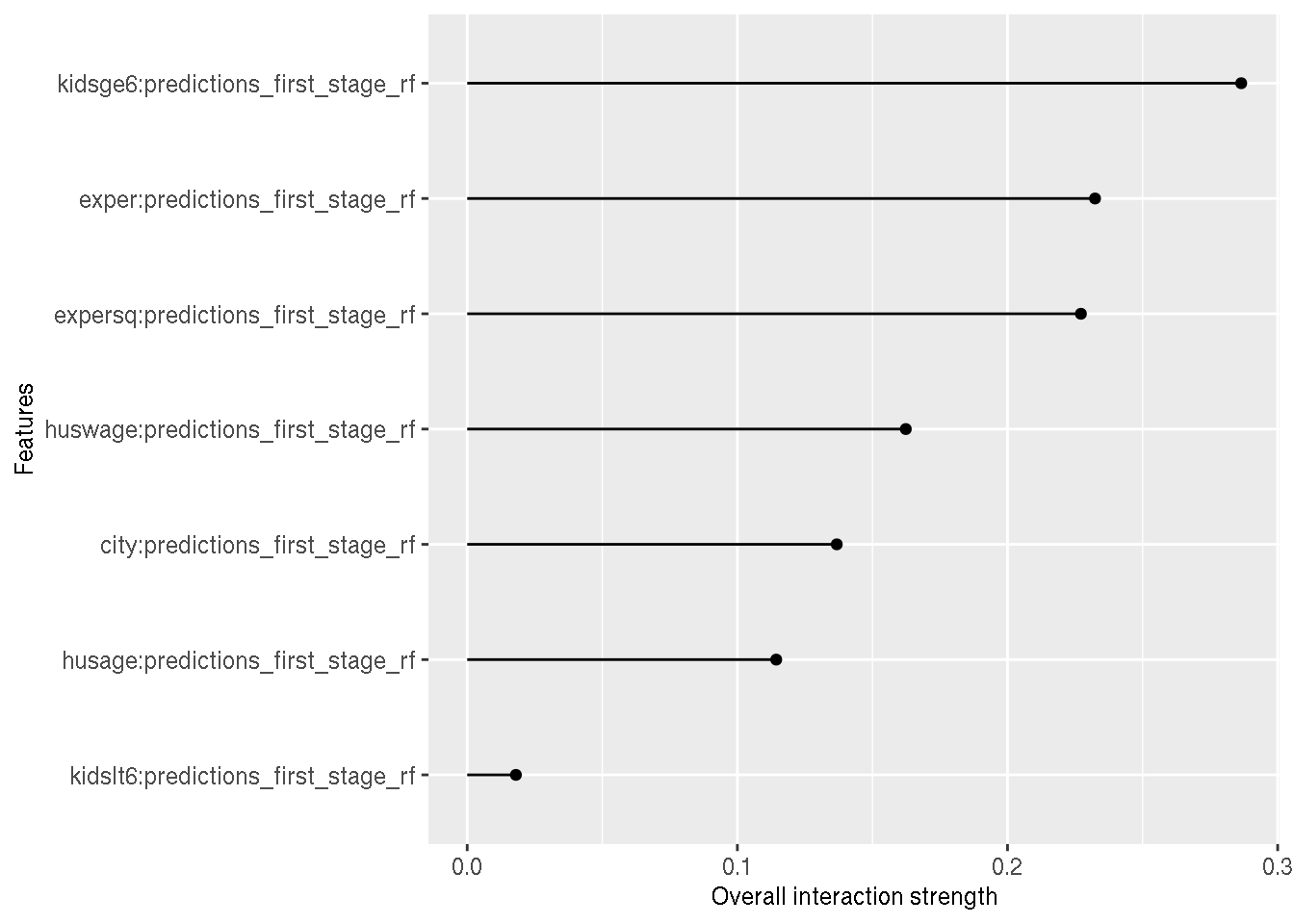
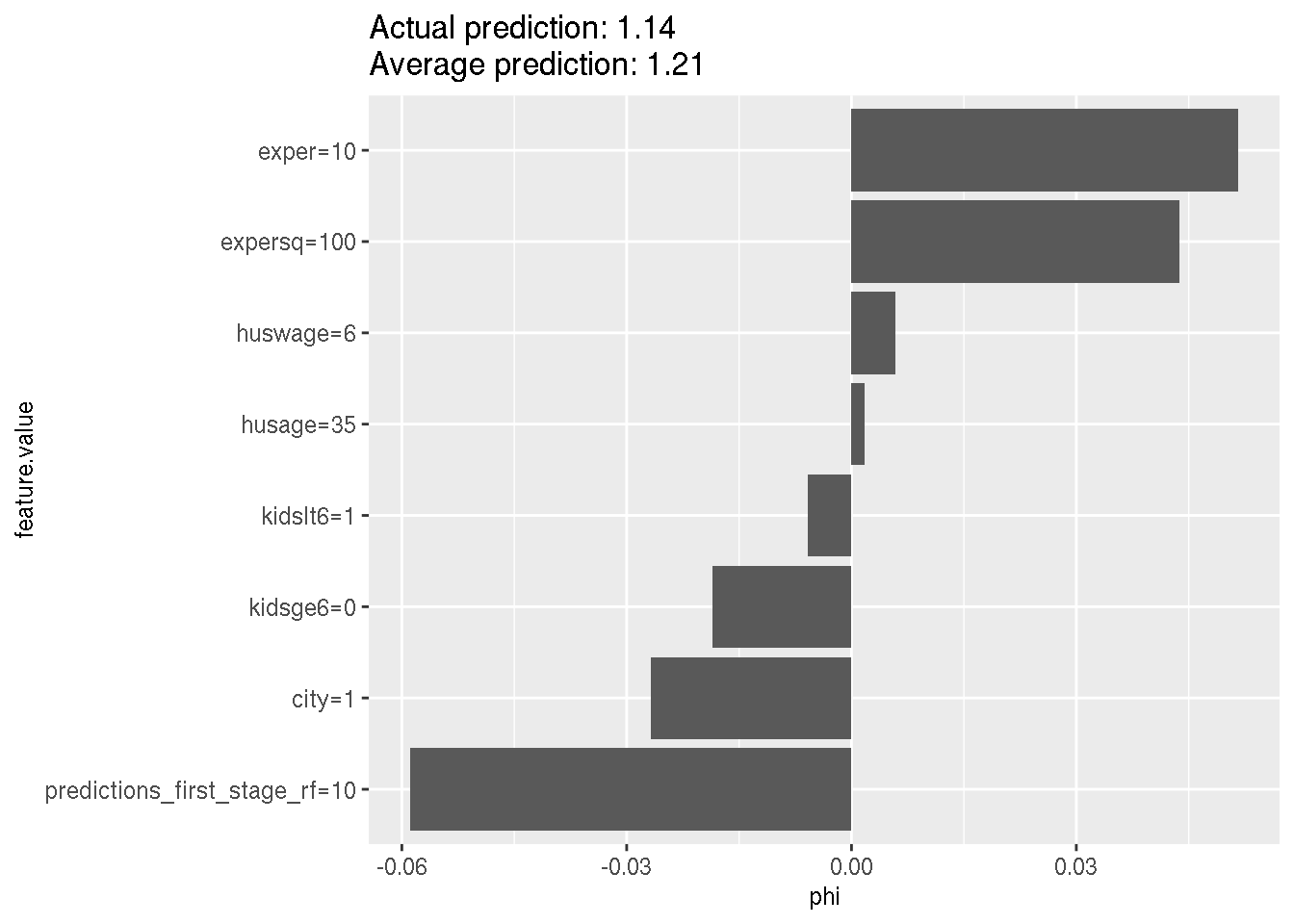
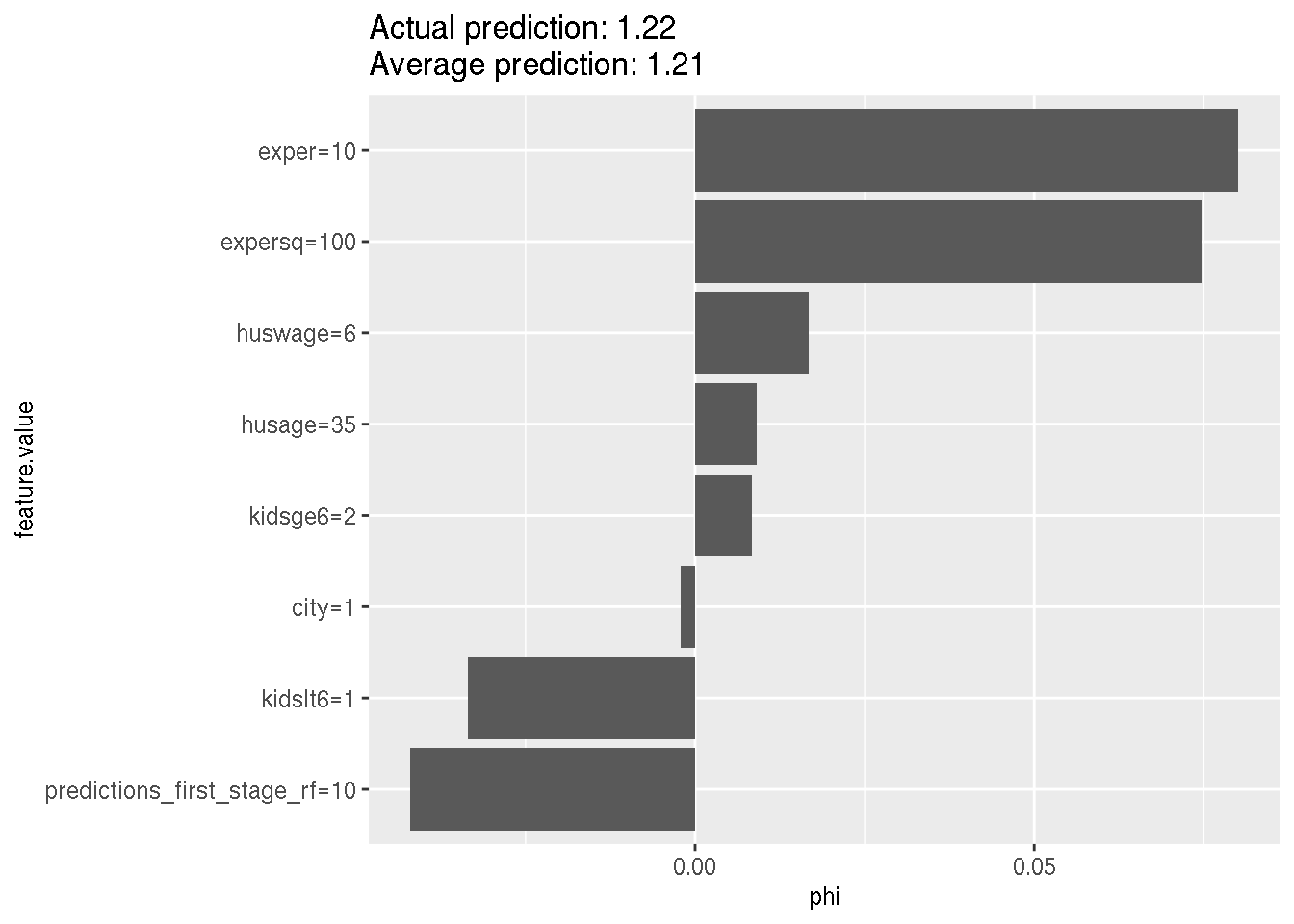
## F-statistic: 5.346 on 8 and 376 DF,  p-value: 2.251e-06

The results are pretty similar. Now, why not go a bit further and use a random forest for the second stage as well?

Two-stage random forests

I have tried to find literature on this, but did not find anything that really fits what I’ll be doing here. Honestly, I don’t know if this is sound theoretically, but it does have intuitive appeal. Using random forests instead of the linear regressions of each stages poses at least the following question: how can we interpret the results of the second stage? As you have seen above, interpretation of the coefficients and standard errors is important, and random forests do not provide this. My idea is to use explainability techniques of black box models, such as partial dependence plots. In this setting, the whole first stage could be interpreted as a feature engineering step. Let’s do it and see what happens.

We already have the first step from before, so let’s go straight to the first step: 

second_stage_rf_rf <- randomForest(lwage ~ exper + expersq + kidslt6 + kidsge6 + 
                                       husage + huswage + city + predictions_first_stage_rf,
                  data = train)

Let’s now use the {iml} package for explainability. Let’s start first by loading the package, defining a predictor object, and then get model-agnostic feature importance: 

library("iml")

predictor <- Predictor$new(
  model = second_stage_rf_rf, 
  data = select(test, exper, expersq,
                kidslt6, kidsge6,
                husage, huswage, city,
                predictions_first_stage_rf), 
  y = test$lwage, 
  predict.fun = predict,
  class = "regression"
  )

The plot below shows the ratio of the original model error and model error after permutation. A higher value indicates that this feature is important: 

imp_rf <- FeatureImp$new(predictor, loss = "rmse")

plot(imp_rf)

According to this measure of feature importance, there does not seem to be any feature that is important in predicting log wage. This is similar to the result we had with linear regression: most coefficients were not statistically significant, but some were. Does that mean that we should not trust the results of linear regression? After all, how likely is it that log wages can be modeled as a linear combination of features?

Let’s see if the random forest was able to undercover strong interaction effects: 

interactions <- Interaction$new(predictor, feature = "predictions_first_stage_rf")

plot(interactions)

This can seem to be a surprising result: education interacts strongly with the number of kids greater than 6 in household. But is it? Depending on a woman’s age, in order to have 2 or 3 kids with ages between 6 and 18, she would have needed to start having them young, and thus could not have pursued a master’s degree, or a PhD. The interaction strength is measured as the share of variance that is explained by the interaction.

Let’s now take a look at the partial dependence plots and individual conditional expectation curves. Let me quote the advantages of pdps from Christoph Molnar’s book on interpretable machine learning:

The calculation for the partial dependence plots has a causal interpretation. We intervene on a feature and measure the changes in the predictions. In doing so, we analyze the causal relationship between the feature and the prediction. The relationship is causal for the model – because we explicitly model the outcome as a function of the features – but not necessarily for the real world!

That sounds good. If we can defend the assumption that our instruments are valid, then the relationship should between the feature and the prediction should be causal, and not only for the model. However, pdps have a shortcoming. Again, quoting Christoph Molnar:

The assumption of independence is the biggest issue with PD plots. It is assumed that the feature(s) for which the partial dependence is computed are not correlated with other features.

Let’s take a look at the correlation of features 

corr_vars <- cor(select(test, exper, expersq,
                        kidslt6, kidsge6,
                        husage, huswage, city,
                        predictions_first_stage_rf)) %>% 
    as.data.frame() %>% 
    rownames_to_column() %>% 
    pivot_longer(-rowname, names_to = "vars2") %>% 
    rename(vars1 = rowname)

head(corr_vars)
## # A tibble: 6 x 3
##   vars1 vars2    value
##   <chr> <chr>    <dbl>
## 1 exper exper    1    
## 2 exper expersq  0.959
## 3 exper kidslt6 -0.272
## 4 exper kidsge6 -0.360
## 5 exper husage   0.487
## 6 exper huswage -0.181
corr_vars %>% 
    mutate(value = abs(value)) %>% 
    filter(value != 1, value > 0.2) %>%
    filter(vars1 == "predictions_first_stage_rf")
## # A tibble: 5 x 3
##   vars1                      vars2   value
##   <chr>                      <chr>   <dbl>
## 1 predictions_first_stage_rf expersq 0.243
## 2 predictions_first_stage_rf kidslt6 0.292
## 3 predictions_first_stage_rf husage  0.217
## 4 predictions_first_stage_rf huswage 0.494
## 5 predictions_first_stage_rf city    0.369

Only 5 variables have a correlation greater than 0.2 with education, and the one with highest correlation is the husband’s wage. It would seem that this situation is ideal to use pdps and ice curves. Before computing them however, let’s read about ice curves:

Individual conditional expectation curves are even more intuitive to understand than partial dependence plots. One line represents the predictions for one instance if we vary the feature of interest.

however:

ICE curves can only display one feature meaningfully, because two features would require the drawing of several overlaying surfaces and you would not see anything in the plot. ICE curves suffer from the same problem as PDPs: If the feature of interest is correlated with the other features, then some points in the lines might be invalid data points according to the joint feature distribution. If many ICE curves are drawn, the plot can become overcrowded and you will not see anything. The solution: Either add some transparency to the lines or draw only a sample of the lines. In ICE plots it might not be easy to see the average. This has a simple solution: Combine individual conditional expectation curves with the partial dependence plot. Unlike partial dependence plots, ICE curves can uncover heterogeneous relationships.

So great, let’s go: 

inst_effect <- FeatureEffect$new(predictor, "predictions_first_stage_rf", method = "pdp+ice")

plot(inst_effect)

Interesting, we see that the curves are fairly similar, but there seem to be two groups: one group were adding education years increases wages, and another where the effect seems to remain constant.

Let’s try to dig a bit deeper, and get explanations for individual predictions. For this, I create two new observations that have exactly the same features, but one without children older than 6 and another with two children older than 6: 

(new_obs <- data.frame(
    exper = rep(10, 2),
    expersq = rep(100, 2),
    kidslt6 = rep(1, 2),
    kidsge6 = c(0, 2),
    husage = rep(35, 2),
    huswage = rep(6, 2),
    city = rep(1, 2),
    predictions_first_stage_rf = rep(10, 2)
))
##   exper expersq kidslt6 kidsge6 husage huswage city
## 1    10     100       1       0     35       6    1
## 2    10     100       1       2     35       6    1
##   predictions_first_stage_rf
## 1                         10
## 2                         10

Let’s see what the model predicts: 

predict(second_stage_rf_rf, newdata = new_obs)
##        1        2 
## 1.139720 1.216423

Let’s try to understand the difference between these two predictions. For this, we will be using Shapley values as described here. Shapley values use game theory to compute the contribution of each feature towards the prediction of one particular observation. Interpretation of the Shapley values is as follows (quoting Christoph Molnar’s book): Given the current set of feature values, the contribution of a feature value to the difference between the actual prediction and the mean prediction is the estimated Shapley value.

Let’s compute the Shapley values of all the features: 

shapley_1 <-  Shapley$new(predictor, x.interest = new_obs[1, ], sample.size = 100)
shapley_2 <-  Shapley$new(predictor, x.interest = new_obs[2, ], sample.size = 100)
plot(shapley_1)

plot(shapley_2)

The average prediction is 1.21 and the prediction for the first new observation is 1.14, which is 0.07 below the average prediction. This difference of 0.07 is the sum of the Shapley values. For the second observation, the prediction is 1.22, so 0.01 above the average prediction. The order and magnitude of contributions is not the same as well; and surprisingly, the contribution of the instrumented education to the prediction is negative.

Ok, let’s end this here. I’m quite certain that explainability methods will help econometricians adopt more machine learning methods in the future, and I am also excited to see the research of causality in machine learning and AI continue.